Hace ya unos meses vi a un usuario de Twitter llamado Playmobil que compartía un Excel que nos ayudaba a construir una base de maná sólida basada en números teniendo en cuenta varias variables como la curva y el coste de las cartas.
Desde entonces he dejado de crear bases de mana basadas en la simetría, prueba y error, intuición o creencias, para hacerlas basadas en las probabilidades, en los números de este Excel.
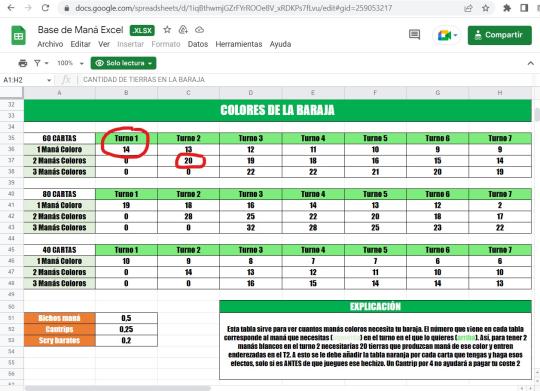
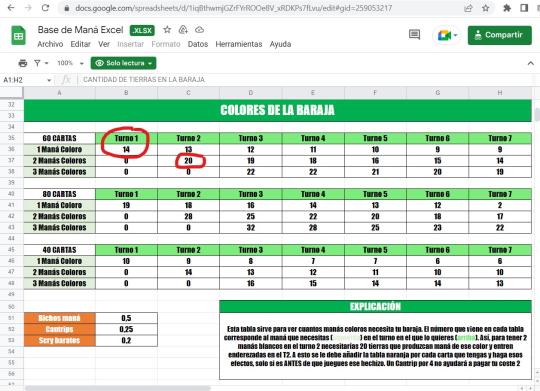
Como no quería estar acudiendo al Excel cada vez que quisiera montar una base de maná, me quede con un par de números mágicos, que me permitían resolver la mayoría de casos. Esos números son el 14 y el 20.
…
Hace ya unos meses vi a un usuario de Twitter llamado Playmobil que compartía un Excel que nos ayudaba a construir una base de maná sólida basada en números teniendo en cuenta varias variables como la curva y el coste de las cartas.
Desde entonces he dejado de crear bases de mana basadas en la simetría, prueba y error, intuición o creencias, para hacerlas basadas en las probabilidades, en los números de este Excel.
Como no quería estar acudiendo al Excel cada vez que quisiera montar una base de maná, me quede con un par de números mágicos, que me permitían resolver la mayoría de casos. Esos números son el 14 y el 20.
Estos números nos van a dar más de un 80% en una baraja de 60 cartas. Por ejemplo:
- Si tenemos cartas azules de coste uno y queremos poder jugarlas con estas garantías, debemos meter 14 tierras enderezadas que produzcan maná azul.
- Si la carta azul que queremos jugar en el turno dos es de coste dos, necesitaremos una carta menos 14 -1 =13 tierras. Y como se trata del turno dos, ya no hace falta que sean tierras enderezadas, porque podremos jugarlas tapeadas en el primer turno.
- Si queremos jugar una carta azules de coste tres en el tercer turno: 14 -2 = 12, son las tierras azules que deberemos incluir en nuestra lista principal.
Por lo tanto la fórmula sería: 14 -(turno-1).
Con el 20 pasa lo mismo, pero para cartas de doble coste y a partir del segundo turno como es lógico. Por ejemplo:
- Si queremos jugar una criatura blanca de doble coste blanco, debemos jugar 20 tierras blancas que produzcan blanco y además 13 (14 -1) de estas tierras deben entrar enderezadas para poder jugar con estas garantías nuestra criatura blanca de doble coste.
- Si queremos jugar un doble coste blanco en el tercer turno, necesitaremos 19 (20 -1) tierras que produzcan blanco.
- 18 (20 -2) para un doble coste blanco en el cuarto turno.
Por lo tanto la fórmula sería: 20 -(turno-2).
Haremos un inciso para explicar esto de "estas garantías". Si trabajamos con estos números es porque nos resultan cómodos para construir una baraja donde una de cada cinco veces se vaya a comportar como nosotros hemos previsto.
Podríamos incrementar el número mágico para tener mayores probabilidades, pero ya no serían números tan flexibles y viables para abordar todas las variables que, como veremos a continuación, no solo son para ajustar la base de maná.
Como hemos anticipado antes, estos números mágicos también nos sirven para ajustar el resto de cartas de nuestra baraja, no solo la base de maná. Por ejemplo:
- Si queremos jugar un coste dos con estas garantías, necesitaremos configurar nuestra baraja con 13 (14 -1) tierras enderezadas. Y este es un requisito muy a tener en cuenta para no pasarnos incluyendo un exceso de tierras tapeadas.
- Si queremos jugar una criatura de coste dos después de jugar la saga de Kumano que pone un contador a la siguiente criatura que juguemos, ¿cuántas hacen falta? 13 (14 -1).
¿Para jugar esta saga roja de coste uno? 14 tierras rojas destapeadas.
Esta regla de tres o fórmula simple ha mejorado por mucho mi juego. Ya no pienso que me he equivocado metiendo menos tierras de las que debía porque el azar me ha jugado una mala pasada.
Estamos de acuerdo en que el azar puede traicionarte, pero también se ceba con nuestro rival indistintamente. Por lo tanto, para mí es una variable que no puedes manejar y que tiende al 50% entre robar bien y mal. El azar en uno de sus extremos solo sirve para poner a prueba tu templanza.
A nosotros nos interesan las probabilidades y que los números de la cartas que llevamos en nuestra baraja tengan cierta lógica y garantías, nada de conjeturas, intuiciones ni simetrías ni creencias. Magic son números y si los tienes en cuenta, las probabilidades estarán de tu lado.
Prueba a usar estos números mágicos 14 y 20 y déjame un comentario de como te ha ido. Hasta la próxima.
Welcome to MTGsearch.it 3.0
—MTG's first social network- Posts from other players.
- The latest Magic expansions for the Standard and Explorer player.
- The deck archetypes currently being played in MTG Arena, with a list proposed by our Ai.
- The decks uploaded by other players on this platform.
- A store where you can acquire experience points, level up and more things that we will be adding.
- A standard deck builder.
- A list of users of this social network ordered by the most recent date of the last one they published.
- Access to your user profile where you can change your icon, set a page header and background.
- And a settings section where you can change the theme from dark to light and choose the main color of the platform.
- Finally, we invite you to post something that you think might be interesting to share with other users.
This information will only be visible for tiers 0 and 1.

Lobo Blanco
Tier: 9Magic son números
Comment?
😍


Lobo Blanco
Tier: 9Magic are Numbers
A few months ago I saw a Twitter user named Playmobil sharing an Excel that helped us build a solid mana base based on numbers by taking into account various variables like curve and card cost.
Since then I have stopped creating mana bases based on symmetry, trial and error, intuition or beliefs, to make them based on probabilities, on the numbers in this Excel.
Since I didn't want to go to Excel every time I wanted to set up a mana base, I kept a couple of magic numbers, which allowed me to solve most cases. Those numbers are 14 and 20.
… A few months ago I saw a Twitter user named Playmobil sharing an Excel that helped us build a solid mana base based on numbers by taking into account various variables like curve and card cost.
Since then I have stopped creating mana bases based on symmetry, trial and error, intuition or beliefs, to make them based on probabilities, on the numbers in this Excel.
Since I didn't want to go to Excel every time I wanted to set up a mana base, I kept a couple of magic numbers, which allowed me to solve most cases. Those numbers are 14 and 20.
These numbers are going to give us more than 80% in a deck of 60 cards. For example:
- If we have one cost blue cards and we want to be able to play them with these guarantees, we must put 14 untapped lands that produce blue mana.
- If the blue card that we want to play on turn two is cost two, we will need a card minus 14 -1 = 13 lands. And since it's turn two, they don't need to be untapped lands anymore, because we'll be able to play them tapped on turn one.
- If we want to play a three-cost blue card on the third turn: 14 -2 = 12, these are the blue lands that we must include in our main list.
Therefore the formula would be: 14 -(turn-1).
The same thing happens with 20, but for double-cost cards and from the second turn, of course. For example:
- If we want to play a white creature with double white cost, we must play 20 white lands that produce white and also 13 (14 -1) of these lands must enter untapped to be able to play our double cost white creature with these guarantees.
- If we want to play a double white cost on the third turn, we will need 19 (20 -1) lands that produce white.
- 18 (20 -2) for a double white cost on the fourth turn.
Therefore the formula would be: 20 -(turn-2).
We will make a subsection to explain this "these guarantees". If we work with these numbers it is because they are comfortable for us to build a deck where one out of every five times it will behave as we have foreseen.
We could increase the magic number to have higher odds, but it would no longer be as flexible and workable numbers to address all the variables that, as we will see below, are not only for adjusting the mana base.
As we have anticipated before, these magic numbers also help us adjust the rest of the cards in our deck, not just the mana base. For example:
- If we want to play a cost two with these guarantees, we'll need to set up our deck with 13 (14 -1) untapped lands. And this is a very important requirement to keep in mind so as not to overdo it by including an excess of capped lands.
- If we want to play a cost two creature after playing the Kumano Saga that puts a counter on the next creature we play, how many do we need? 13 (14 -1).
To play this cost one red saga? 14 red lands uncovered.
This rule of three or simple formula has greatly improved my game. I no longer think that I have made a mistake putting in less land than I should have because chance has played a trick on me.
We agree that chance can betray you, but it also preys on our rival indistinctly. Therefore, for me it is a variable that you cannot manage and that tends to 50% between stealing well and poorly. Chance at one of its extremes only serves to test your temperance.
We are interested in the probabilities and that the numbers of the cards that we carry in our deck have a certain logic and guarantees, no conjectures, intuitions, symmetries or beliefs. Magic are numbers and if you take them into account, the odds will be on your side.
Try using these magic numbers 14 and 20 and leave me a comment on how it went. Until next time.
Since then I have stopped creating mana bases based on symmetry, trial and error, intuition or beliefs, to make them based on probabilities, on the numbers in this Excel.
Since I didn't want to go to Excel every time I wanted to set up a mana base, I kept a couple of magic numbers, which allowed me to solve most cases. Those numbers are 14 and 20.
… A few months ago I saw a Twitter user named Playmobil sharing an Excel that helped us build a solid mana base based on numbers by taking into account various variables like curve and card cost.
Since then I have stopped creating mana bases based on symmetry, trial and error, intuition or beliefs, to make them based on probabilities, on the numbers in this Excel.
Since I didn't want to go to Excel every time I wanted to set up a mana base, I kept a couple of magic numbers, which allowed me to solve most cases. Those numbers are 14 and 20.
These numbers are going to give us more than 80% in a deck of 60 cards. For example:
- If we have one cost blue cards and we want to be able to play them with these guarantees, we must put 14 untapped lands that produce blue mana.
- If the blue card that we want to play on turn two is cost two, we will need a card minus 14 -1 = 13 lands. And since it's turn two, they don't need to be untapped lands anymore, because we'll be able to play them tapped on turn one.
- If we want to play a three-cost blue card on the third turn: 14 -2 = 12, these are the blue lands that we must include in our main list.
Therefore the formula would be: 14 -(turn-1).
The same thing happens with 20, but for double-cost cards and from the second turn, of course. For example:
- If we want to play a white creature with double white cost, we must play 20 white lands that produce white and also 13 (14 -1) of these lands must enter untapped to be able to play our double cost white creature with these guarantees.
- If we want to play a double white cost on the third turn, we will need 19 (20 -1) lands that produce white.
- 18 (20 -2) for a double white cost on the fourth turn.
Therefore the formula would be: 20 -(turn-2).
We will make a subsection to explain this "these guarantees". If we work with these numbers it is because they are comfortable for us to build a deck where one out of every five times it will behave as we have foreseen.
We could increase the magic number to have higher odds, but it would no longer be as flexible and workable numbers to address all the variables that, as we will see below, are not only for adjusting the mana base.
As we have anticipated before, these magic numbers also help us adjust the rest of the cards in our deck, not just the mana base. For example:
- If we want to play a cost two with these guarantees, we'll need to set up our deck with 13 (14 -1) untapped lands. And this is a very important requirement to keep in mind so as not to overdo it by including an excess of capped lands.
- If we want to play a cost two creature after playing the Kumano Saga that puts a counter on the next creature we play, how many do we need? 13 (14 -1).
To play this cost one red saga? 14 red lands uncovered.
This rule of three or simple formula has greatly improved my game. I no longer think that I have made a mistake putting in less land than I should have because chance has played a trick on me.
We agree that chance can betray you, but it also preys on our rival indistinctly. Therefore, for me it is a variable that you cannot manage and that tends to 50% between stealing well and poorly. Chance at one of its extremes only serves to test your temperance.
We are interested in the probabilities and that the numbers of the cards that we carry in our deck have a certain logic and guarantees, no conjectures, intuitions, symmetries or beliefs. Magic are numbers and if you take them into account, the odds will be on your side.
Try using these magic numbers 14 and 20 and leave me a comment on how it went. Until next time.

Lobo Blanco
Tier: 9Probabilidad usando Compañía reunida
Para esta carta no me sonaba que haya que llevar tantas criaturas en la base principal de la baraja. En una primera búsqueda, en un artículo de CFB de Frank Karsten, he encontrado esto:
Con 22 tienes un 5% de fallar por completo, un 21% de poner una criatura en juego y un 74% de poner dos.
(Son % razonables, aunque yo trataría de situarme en un 85%. Seguiré buscando para contrastar esto).
Con 22 tienes un 5% de fallar por completo, un 21% de poner una criatura en juego y un 74% de poner dos.
(Son % razonables, aunque yo trataría de situarme en un 85%. Seguiré buscando para contrastar esto).



Lobo Blanco
Tier: 9Standard Jund Reanimator
He visto jugar a Mati su Jund Reanimator y como no me exigía muchos comodines para la mayoría de las cartas nuevas, no he podido resistir a probarla.
Y después de la primera partida, puedo decir que a pesar de que yo juego menos pay-lands, reanimar al demonio por 7 vidas es muy doloroso. Lo gracioso es que no pude pegar ni una sola vez con el demonio al ver que mi rival se quedaba siempre con cuatro tierras disponibles. Hasta el punto que pude bajar un titán a pelo y copiarlo con el goblin... :P
Y después de la primera partida, puedo decir que a pesar de que yo juego menos pay-lands, reanimar al demonio por 7 vidas es muy doloroso. Lo gracioso es que no pude pegar ni una sola vez con el demonio al ver que mi rival se quedaba siempre con cuatro tierras disponibles. Hasta el punto que pude bajar un titán a pelo y copiarlo con el goblin... :P
MTGsearch.it > decks > deck
S Jund Reanimator 1.0 by Lobo Blanco